Turunan suatu fungsi berawal dari sebuah permasalahan yang berkaitan dengan garis singgung. Nilai turunan didekati dengan konsep limit untuk suatu selang nilai mendekati nol. Turunan fungsi trigonometri merupakan sebuah permasalahan turunan yang melibatkan fungsi trigonometri seperti sinus, cosinus, tan, dan lain sebagainya. Sehingga agar dapat menyelesaikan soal turunan fungsi trigonometri, sobat idschool membutuhkan pengetahuan dasar fungsi trigonometri dan bagaimana cara menurunkan suatu fungsi.
Sebelumnya, ingat kembali apa itu turunan dari suatu fungsi. Definisi turunan pertama suatu fungsi f adalah fungsi lain f’ (dibaca: f aksen) yang nilainya pada sebarang bilangan c adalah f’(c) yang dinyatakan dalam persamaan di bawah.
Dari definisi turunan tersebut dapat digunakan untuk menentukan turunan fungsi dan berkembang teorema-teorema yang berguna untuk mempermudah menentukan turunan suatu fungsi. Begitu juga pada fungsi trigonometri, bentuk turunan fungsi trigonometri dapat diketahui melalui definis turunan. Bagaimana cara menentukan turunan fungsi trigonometri? Sobat idschool dapat mencari tahu caranya melalui ulasan dibawah.
Baca Juga: Cara Menentukan Nilai Limit Suatu Fungsi Trigonometri
Rumus Turunan Fungsi Trigonometri Dasar
Sebelumnya, ingat kembali bagaimana cara memperoleh turunan dari suatu fungsi. Turunan dari sebuah fungsi p(x) = x3 + 5x adalah p’(x) = 3x2 + 5 yang dapat diperoleh dari definisi turunan. Selain itu, sobat idschool dapat juga langsung menggunakan sebuah teorema aturan pangkat yang sudah terbukti kebenarannya. Bunyi teorema aturan pangkat terdapat seperti pernyataan berikut.
Contoh: pada fungsi f(x) = x3 nilai n = 3, sehingga turunan dari f(x) = x3 adalah f’(x) = 3x3–1 = 3x2. Contoh lain, pada fungsi g(x) = 5x nilai n = 1, sehingga turunan dari g(x) = 5x adalah g’(x) = 1 · 5x1–1 = 5x0 = 3 (ingat, hasil bilangan dengan pangkat adalah 1).
Berdasarkan teorema aturan jumlah, jika f(x) dan g(x) adalah fungsi adalah fungsi-fungsi yang terdiferensialkan maka (f+g)’(x) = f’(x) + g’(x). Dari teorema tersebut dapat digunakan untuk mengetahui hasil turunan dari fungsi p(x) = x3 + 5x adalah p’(x) = 3x2 + 5.
Cara Mendapatkan Hasil Turunan Fungsi Trigonometri
Selanjutnya bagaimana untuk fungsi trigonometri? Sobat idschool dapat menggunakan definisi turunan sebagai awal permulaan. Sebagai contoh, akan dicari turunan dari fungsi sin x.
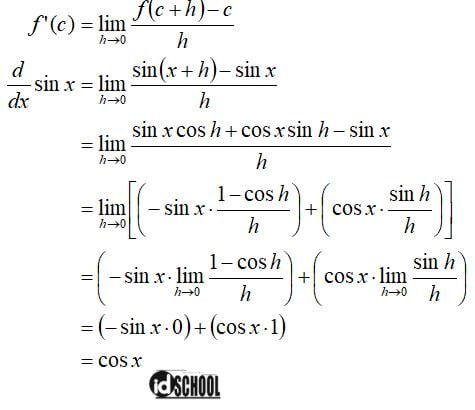
Hasil akhir dari proses tersebut menunjukkan bahwa turunan dari f(x) = sin x adalah f’(x) = cos x. Dengan cara yang sama dapat diperoleh bahwa turunan dari f(x) = cos x adalah f’(x) = –sin x.
Selanjutnya, sobat idschool mungkin tidak perlu mencari turunan fungsi trigonometri dasar menggunakan definisi turunan karena prosesnya tidak akan menguntungkan. Sobat idschool hanya perlu mengingat bentuk turunan fungsi trigonometri dasar yang berjumlah enam.
Untuk memudahkan mengingat, perhatikan tabel rumus turunan fungsi trigonometri dasar berikut.
Rumus dasar fungsi trigonometri di atas akan mempermudah mengerjakan soal turunan fungsi trigonometri yang lebih sulit.
Agar dapat menyelesaikan turunan fungsi trigonometri dengan baik, sobat idschool juga perlu paham bagaimana dasar penurunan suatu fungsi. Selain itu, sobat idschool juga perlu memahami aturan apa saja yang terdapat pada teorema-teorema turunan.
Baca Juga: Materi Dasar Turunan Fungsi dan Teorema/Aturan Penting di Dalamnya
Contoh Soal dan Pembahasan
Beberapa contoh soal di bawah dapat sobat idschool gunakan sebagai tolak ukur pemahaman bahasan di atas. Keberhasilan soal dapat menjadi tanda bahwa cukup memahami suatu bahasan. Contoh-contoh soal turunan fungsi trigonometri yang diberikan di bawah dilengkapi dengan pembahasan. Sobat idschool dapat menggunakan pembahsan tersebut sebagai parameter keberhasilan mengerjakan soal. Selamat berlatih!
Contoh 1 – Soal Turunan Fungsi Trigonometri
Turunan pertama dari y = 1/4 sin 4x adalah ….
A. –1/4 cos 4x
B. 1/4 cos 4x
C. –4 cos 4x
D. cos 4x
E. 4 cos 4x
Pembahasan:
Misalkan:
- u = 4x → y = 1/4 sin u
Sehingga, dapat dipeorleh nilai dy/du dan du/dx seperti berikut.
- dy/du = 1/4 cos u
- du/dx = 4
Mencari turunan pertama fungsi y = 1/4 sin 4x (dy/dx):
dy/dx = dy/du · du/dx
dy/dx = 1/4 cos u · 4
= cos u
= cos 4x
Jadi, turunan pertama dari y = 1/4 sin 4x adalah cos 4x.
Jawaban: D
Contoh 2 – Soal Turunan Fungsi Trigonometri

Pembahasan:
Misalkan:
- u = 2x–5/3x–1
- f(x) = cos2u
Mencari turunan pertama fungsi f(x):

Jawaban: B
Demikianlah tadi bahasan materi turunan fungsi trigonometri yang dilengkapi dengan contoh soal beserta pembahasan. Terimakasih sudah mengunjungi idschool(dot)net, semoga bermanfaat.
Baca Juga: Aplikasi Turunan – Mencari Luas Maksimum/Minimum Suatu Daerah
Sumber gini.com



EmoticonEmoticon